No sistema solar, os astros descrevem órbitas elípticas. Uma elipse com um dos focos na origem pode ser descrita pela equação:
$$ r = \frac{a (1-\varepsilon^2)}{1+\varepsilon \cos(\nu - \varpi)}\, ,$$
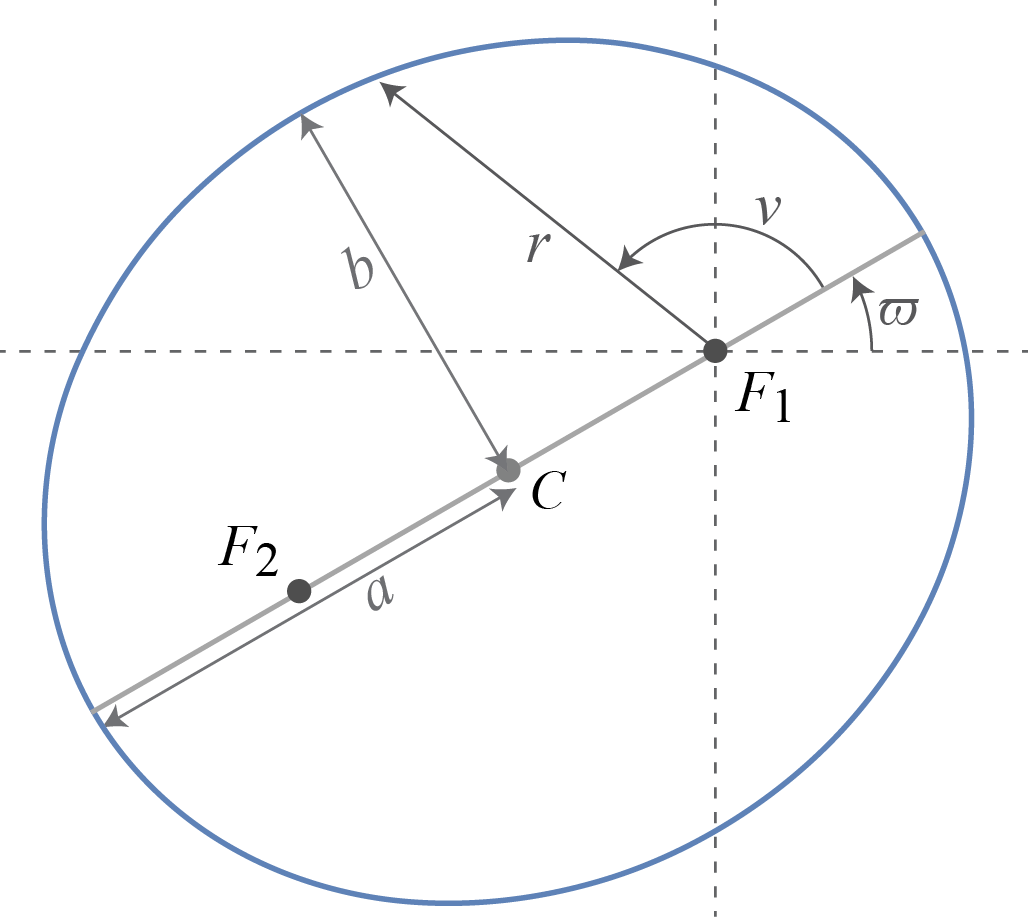
onde $\varepsilon$ é a excentricidade da elipse, $a$ é o semi-eixo maior e $\varpi$ é a longitude do perihélio, e $\nu$ é o ângulo medido a partir do perihélio (chamado “anomalia verdadeira”). Por simplicidade, vamos considerar apenas os objetos com plano orbita próximo da eclíptica, isto é, com inclinação $\lesssim$ 15$^\circ$.
 |
$F_1$ e $F_2$ são os focos da Elipse, $F_1$ está na origem do sistema de coordenadas (representados pelas linhas perpendiculares tracejadas). $a$ e $b$ são os semi-eixos maior e menor, respectivamente. $C$ é o centro da elípse. |
O movimento de um corpo, devido ao campo gravitacional do Sol -- ignorando todos os outros corpos do sistema solar -- é ao longo de uma elipse segundo as Leis de Kepler. Para obtermos o movimento em função do tempo, devemos resolver o chamado problema de dois corpos. Por simplicidade, supomos que o Sol esteja fixo no foco $F_1$. Como a massa de qualquer objeto do sistema solar é muito menor que a massa do Sol, esta aproximação é muito boa.
A descrição mais detalhada do método usado aqui pode ser encontrada nestas nota de aula de Astronomia de Posição. Você também pode ver vários exemplos de órbitas no Sistema Solar (com animações) nesta página.
Nós começamos pelo movimento médio do objeto ao longo de sua órbita:
$$M(t) = M_0 \frac{2\pi\, t}{P} \, ,$$
onde $M_0$ é a posição inicial (a chamada “anomalia média” inicial) e $P$ é o período orbital. Por exemplo, para a Terra, $P = 365,259$ dias; este é o ano sideral (não é o ano trópico que usamos no calendário). O tempo $t$ é medido a partir de algum momento arbitrário que escolhemos.
O próximo passo é calcular a anomalia excêntrica, $E$, dada pela equação:
$$ E - \varepsilon \sin E = M\, .$$
Esta equação é trancendental e não tem solução analítica. Podemos resolvê-la numericamente ou usar alguma aproximação, por exemplo, esta de 4$^{\rm a}$ ordem:
$$E \simeq M + \left(\varepsilon - \frac{3}{24} \varepsilon^3\right)\sin M + \left(\frac{\varepsilon^2}{2}-\frac{\varepsilon^4}{8}\right) \sin 2M + \frac{3\varepsilon^3}{8} \sin 3M + \frac{\varepsilon^4}{3} \sin 4M +\ldots$$
Finalmente, a anomalia verdadeira, $\nu$, é dada por:
$$\tan\left(\frac{\nu}{2}\right) = \sqrt{\frac{1+e}{1-e}} \tan \left(\frac{E}{2} \right) \, .$$
Em coordenadas cartesianas, a posição na órbita é dada por:
$$ \left\{
\begin{array}{l}
x = r \cos \nu\, ;\\
y = r \sin \nu \, .
\end{array}
\right.$$
Para passarmos para um referência geocêntrico, basta fazer uma translação do Sol para a Terra. Em coordenadas cartesianas isto é:
$$ \left\{
\begin{array}{l}
x_p = r_p \cos \nu_p - r_T \cos \nu_T\, ;\\
y_p = r_p \sin \nu_p -r_T \sin \nu_T\, ,
\end{array}
\right.$$
onde $(x_p,\, y_p)$ são as coordenadas geocêntricas e os índices $p$ e $T$ referem-se às coordenadas do planeta (ou qualquer corpo em órbita do Sol) e às coordenadas da Terra, respectivamente.
Para calcularmos as posições, heliocêntricas ou geocêntricas, precisamos dos seguintes dados:
| Símbolo | Descrição | Unidade |
| $a$ | semi-eixo maior | unidade astrônomica (UA) |
| $\varepsilon$ | excentricidade | —— |
| $\varpi$ | longitude do perihélio | grau |
| $P$ | período sideral | dia |
| $L_0$ | longitude inicial | grau |
Como estamos assumindo apenas órbitas no plano da eclíptica, não precisamos da inclinação do plano orbital e da longitude do nodo ascendente.
Gastão B. Lima Neto
Depto. de Astronomia
IAG/USP
05/2020