

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Em geral, os planetas não são acessíveis à observação direta. Porém, muitos deles são grandes o bastante para provocar movimentos da estrela que podem ser observados da Terra.
O gráfico ilustra o movimento de um planeta e de uma estrela ao redor do centro de gravidade do sistema formado por eles.
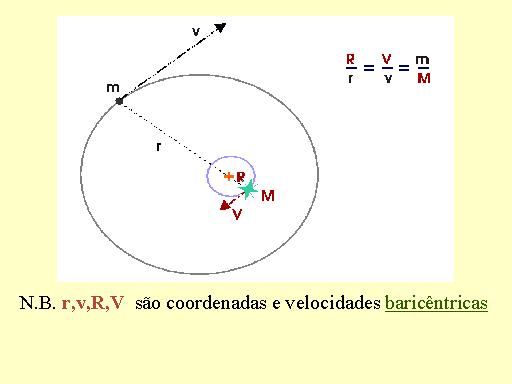
As principais técnicas de busca e descoberta se baseiam na observação dos deslocamentos da estrela ao redor do centro de gravidade do sistema. O método mais antigo é o astrométrico que busca medir o deslocamento geométrico da estrela:
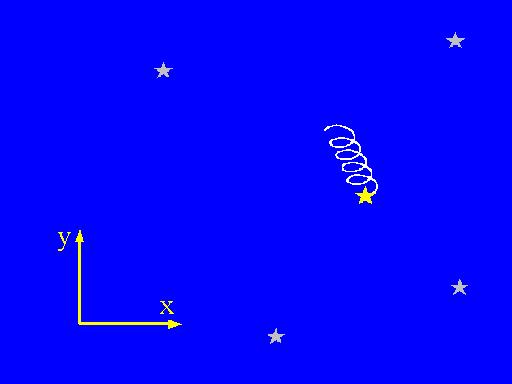
A maneira mais eficiente de investigar o movimento de uma estrela consiste em usar o efeito Doppler para medir a velocidade com que se desloca. Isto é feito medindo-se as variações nas posições das linhas do espectro da estrela. Esta técnica é a responsável pela quase totalidade das descobertas feitas. A velocidade medida resulta da composição de dois movimentos: O movimento da estrela ao redor do centro de gravidade do sistema - uma oscilação parecida com uma senóide - e o movimento de todo o sistema no espaço - uma constante. De fato, o efeito Doppler mede a projeção sobre a linha de visada, da velocidade da estrela em relação ao observador -- que também está em movimento (o que tem que ser considerado detalhadamente na análise das medidas feitas).
Medidas de velocidade radial da estrela 51 Pégaso que tem um planeta bem maior que Saturno executando uma translação completa ao redor da estrela a cada 4 dias e 5,6 horas. A variação total da velocidade da estrela é de 113,6 m/s (409 km/h). As velocidades medidas são representadas pelos pontos amarelos; a linha vermelha indica a variação presumida da velocidade devido ao movimento da estrela ao redor do centro de gravidade do sistema.
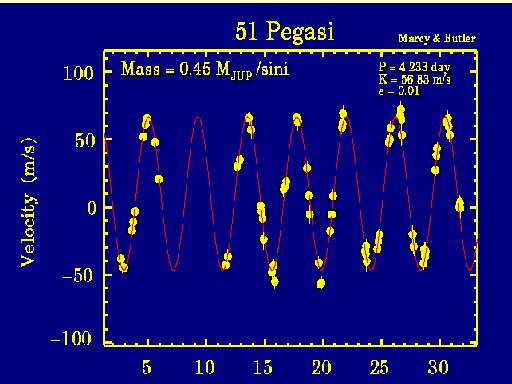
Outra técnica importante para a busca de planetas extra-solares, é a fotometria das estrelas. Se uma estrela tem um planeta e se, em seu movimento, o planeta se interpõe entre a estrela e a Terra, ocorre uma diminuição da quantidade de luz recebida na Terra. A observação dessa diminuição repetidas vezes permite identificar sua causa como sendo o trânsito de um planeta em frente à estrela. A ocorrência do trânsito exige que o sistema tenha uma geometria particular -- o plano do movimento do planeta tem que estar sendo visto de perfil. Em compensação, mesmo a diminuição da luz pelo trânsito de um planeta como a Terra pode ser observada. Essa técnica será usada para a busca de exoplanetas a partir de satélites artificiais da Terra. A missão Corot, da qual o Brasil é um dos países participantes, inclue um satélire a ser lançado no final de 2006 que pretende descobrir um grande número de sistemas planetários extra-solares através de medidas fotométricas.
Para aprofundar as informações que se obtém medindo-se a velocidade de uma estrela, é preciso conhecer a dinâmica que rege o movimento planetário. Essa dinâmica é essencialmente dada pelas leis de Kepler:
1) As trajetórias dos planetas são elipses com um dos fócos no Sol;
2) O raio vetor unindo o planeta ao Sol descreve áreas iguais em tempos iguais (isto é, o momento angular é constante);
3) A razão entre o cubo das distâncias médias dos planetas ao Sol e o quadrado dos períodos dos movimentos é o mesmo para todos os planetas.
CORREÇÃO DE NEWTON À TERCEIRA LEI DE KEPLER
As leis de Kepler são cinemáticas e foram fundamentais para permitir a Newton que descobrisse as leis da mecânica e da gravitação. Com essas leis, Newton mostrou que as duas primeiras leis de Kepler são corretas, mas a terceira lei de Kepler necessita uma pequena correção. Com essa correção, a terceira lei de Kepler se escreve:
isto é, a razão entre o cubo das distâncias médias dos planetas ao Sol e o quadrado dos períodos dos movimentos é apenas aproximadamente o mesmo para todos os planetas. Ela depende também da massa m do planeta que aparece somada à massa da estrela M no fator (M+m). Para Júpiter, esse número é 1,001 (em unidades da massa do Sol) e, para a Terra, 1,000003. Os dois números são quase iguais, mas tem uma diferença que por ser muito pequena não pôde ser percebida por Kepler.
As leis de Kepler se exprimem matematicamente da
seguinte
forma:
Das equações dadas e da geometria da figura podemos escrever uma equação para o vetor Sol-planeta e fazendo sua derivada em relação ao tempo obtemos uma equação para a velocidade do planeta referida à estrela central (por extensão de linguagem: "heliocêntrica"):
Essas equações permitem determinar o movimento do planeta ao redor da estrela. Mas esse movimento não pode ser observado. É preciso pois usá-las para obter o movimento da estrela ao redor do centro de gravidade. Para isso, elas são transformadas com a relação que define a posição do centro de gravidade (e sua derivada em relação ao tempo).
A quantidade K é aproximadamente a metade da amplitude de variação das velocidades radiais medidas (ex: 51Peg). A equação para RV mostra que a curva das velocidades radiais medidas só é uma senóide se a órbita for circular (e=0). Se a órbita é elíptica, a curva é uma senóide deformada. As deformações permitem determinar e e w. Do tipo espectral da estrela podemos estimar o valor de M. Das medidas feitas obtemos 2 parâmetros principais que são o período e K e com eles determinamos os demais parâmetros (supondo que a massa da estrela é bem menor do que a do planeta e M+m @ M).
Essas informações podem ser obtidas se for possível observar os deslocamentos da estrela (astrometria), ou se houver no sistema pelo menos 2 planetas de grande massa cuja interação produza alterações em seus movimentos, cujo reflexo em RV possa ser medido. Esses casos são porém raros, e as tabelas de exoplanetas sempre dão m.sin i ao invés de m. Uma exceção são os planetas da estrela Gliese 876. Essa estrela tem dois planetas que têm interacções gravitacionais fortes e que podem ser medidas e também teve as variações na posição da estrela observadas com o telescópio espacial. Nesse caso, temos uma estimativa direta da massa m.
A dinâmica planetária também permite entender melhor porque só estamos descobrindo planetas tão grandes e tão próximos às estrelas. Usando a terceira lei de Kepler, pode-se ver que a quantidcade observada K é aproximadamente proporcional ao produto m.sin i e inversamente proporcional à raiz quadrada do produto Ma. Então K é maior se m é grande (planeta grande) e se aé pequeno (planeta próximo à estrela). A descoberta também é favorecida quando a estrela é de baixa massa. Estes resultados estão traduzidos de forma gráfica na figura:As tres linhas da figura indicam os valores de K=30 m/s, K=10 m/s e K=3m/s. Para um planeta como Júpiter ao redor de uma estrela como o Sol, e à mesma distância da estrela que Júpiter do Sol, K=13 m/s. Esse valor está acima do limite dos espectrógrafos atuais e um planeta desse tipo poderá ser descoberto acumulando-se observações por um tempo longo (o período de Júpiter ao redor do Sol é 11,8 anos). Já para um planeta como a Terra, a 1 UA de uma estrela como o Sol, K=10 cm/s. Isso é muito menos do que permitem os melhores espectrógrafos e menor do que as variações de velocidade na fotosfera de muitas estrelas devidas à turbulência.
As teorias de formação planetária dizem que eles se formaram por acresção de poeira e gás em um disco ao redor da estrela. Várias estrelas jovens com discos de poeira e gás são conhecidas. O exemplo mais conhecido é b Pic em que a nuvem é visível e onde se suspeita da existência de grandes planetas (jamais observados direta ou indiretamente).
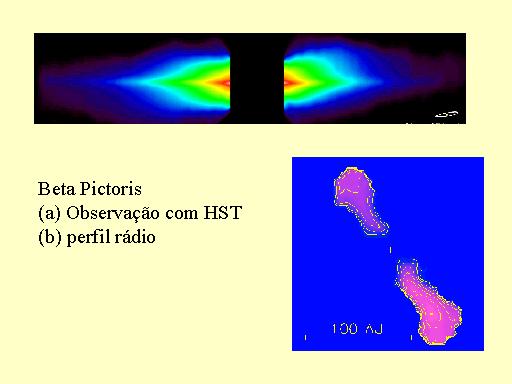
Quando um planeta se forma, ele acreta toda a matéria de um anel circular, abrindo uma clareira anuklar no disco. Acretando a matéria do anel, ele pode chegar ao tamanho de Júpiter.
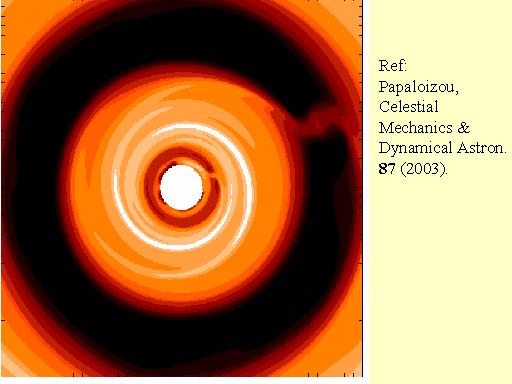
O processo não se interrompe após o esvaziamento do anel. O planeta continua a receber matéria que vem das partes do disco no bordo do anel, através de duas pontes que se formam unindo o planeta ao disco. Os vértices da oval que confina a matéria do planeta são os pontos chamados L1 e L2, descobertos por Euler no problema dos tres corpos.
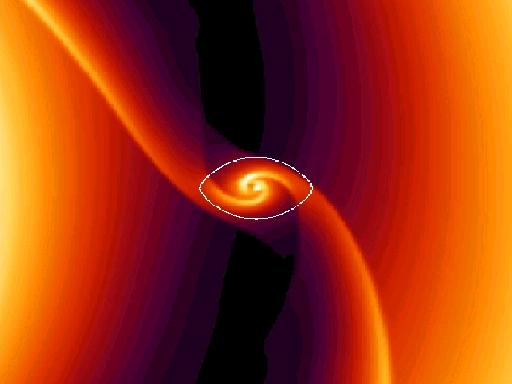
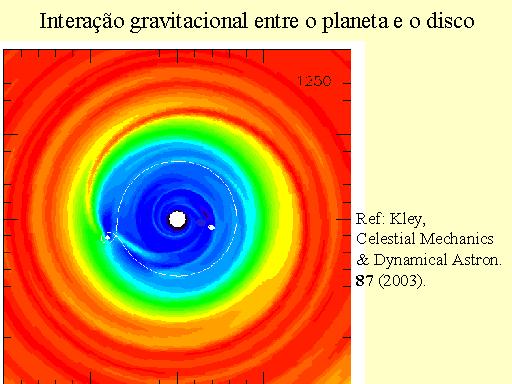
Depois de formado, o planeta continua a interagir com o disco, como o mostra a estrutura espiral que aparece na simulação mostrada na figura. A realidade desse fenômeno pode ser verificada na estrutura observada dos anéis de Saturno em que os braços da espiral são bem visíveis.

;
à esquerda: Movimento em um sistema de referência que está rodando com a mesma velocidade angular que o planeta (e no qual, portanto, o planeta permanece fixo no ponto l). [A linha vermelha é um círculo colocado apenas para referência]. A partícula inicia seu movimento em sentido horário no ponto l, move-se em uma órbita quase circular até se aproximar do planeta (l), e depois é espalhada para fora.à direita: O mesmo movimento representado em um sistema de referência fixo. O planeta se move no círculo vermelho. A partícula se move em sentido anti-horário a partir do ponto l, tem uma forte aproximação ao planeta após cerca de uma órbita e meia, e depois passa a se mover em órbitas bem mais para fora e de maior energia que a sua órbita inicial.
............
| Os movimentos da partícula e do planeta se dão no sentido anti-horário. A partícula aparece se movendo no sentido horário na figura do lado esquerdo porque, lá, o sistema tem eixos girando com a velocidade angular do planeta, que é maior do que a da partícula. |
Isto pode ser estudado de maneira mais completa com as equações da teoria das perturbações. Duas equações imediatas são:
As equações acima traduzem duas leis físicas elementares: "A variação da energia de um ponto material em movimento é igual ao trabalho realizado pelas forças nele aplicadas" e "a variação do momento angular de um ponto material em movimento é igual ao momento das forças nele aplicadas". Sabendo como variam a energia e o momento angular, podemos usar as leis de Newton para saber como mudam o semi-eixo maior e a excentricidade da órbita.
A figura seguinte mostra o efeito do que aconteceria se a interação entre o disco e o planeta consistisse em um impulso em direção contrária à do movimento quando o planeta passasse pela sua maior aproximação ao disco.
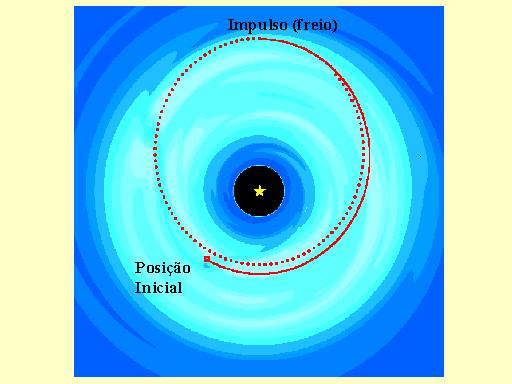
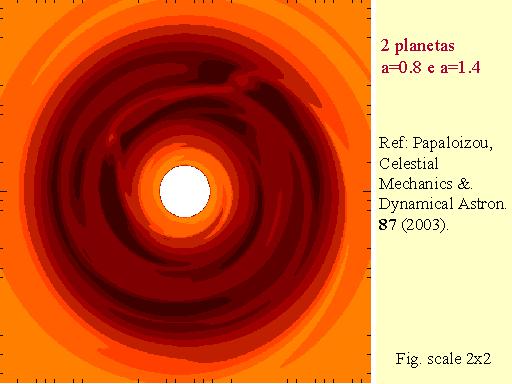 (Ache
os dois planetas !)
(Ache
os dois planetas !)
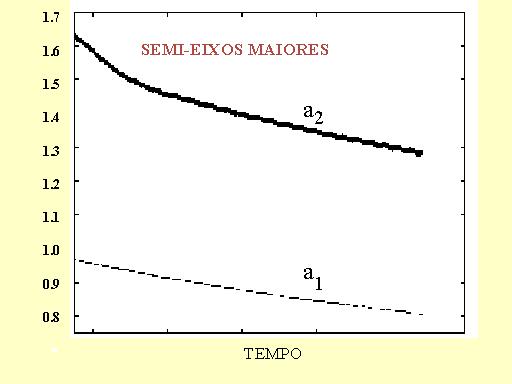
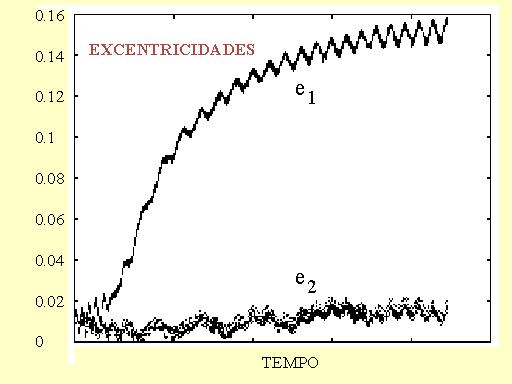
Um ponto importante nesta explicação dos grandes semi-eixos e excentricidades é que os discos de poeira e gás são efêmeros e se dissipam em algumas dezenas de milhões de anos. O efeito sobre o movimento dos planetas cessa com o desaparecimento do disco e os parâmetros orbitais dos exoplanetas que observamos são os que resultaram desse passado (são "fósseis"). A variação dos semi-eixos maiores e das excentricidades em um sistema de dois planetas como o mostrado, é dada nas figuras seguintes.
 ....
....
Além dos planetas conhecidos em órbita ao redor de estrelas da sequência principal, esta tabela inclue os planetas do pulsar B1257+12 e "o planeta" de HD 83443. Neste último caso, o segundo planeta "sumiu" em observações posteriores, indicando que, nesse caso, a "descoberta" ocorreu devido a uma interpretação incorreta das observações.
A imagem mostra o sistema planetário do pulsar B1257+12 com 3 planetas conhecidos em órbita ao redor do pulsar. Para comparação, as órbitas são mostradas superpostas às dos planetas interiores do nosso Sistema Solar.
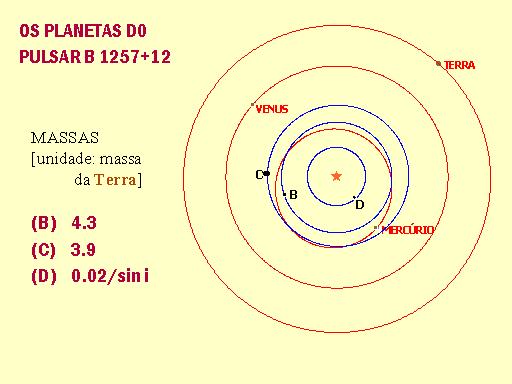
Pulsar B1257+12: Três planetas conhecidos, em órbitas quase circulares (e<0.1), próximas à estrela e com tamanhos próximos ao da órbita de Mercúrio ao redor do Sol. Os dois planetas externos tem massas de mesma ordem de grandeza que a massa da Terra. O planeta mais interno tem massa da ordem da massa da Lua.
Pulsares são estrelas de neutrons em rotação emitindo rádio-ondas na direção do seu eixo magnético. Essa radiação é detectada por rádio-telescópios sempre que o eixo magnético do pulsar estiver apontando na nossa direção. Alguns dos pulsares conhecidos tem uma rotação niforme e dirigem seu feixe de rádio-ondas para nós a cada período (da ordem de milissegundos). A freqüência com que esses pulsos chegam à Terra são afetadas pela velocidade relativa da fonte que os emite (efeito Doppler). Se a fonte está se movendo em nossa direção a freqüência é mais alta (o intervalo de tempo entre a chegada de dois pulsos é menor) do que se estiver se movendo em direção contrária. Com algumas adaptações, as equações obtidas para a velocidade radial das estrelas da seqüência principal com planetas se aplica neste caso.
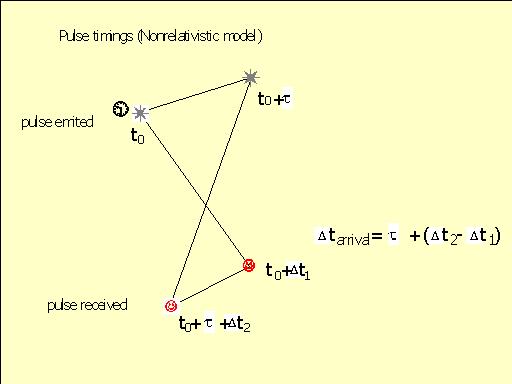
A geometria da figura permite obter algumas relações imediatas. Nessas equações RV é a componente radial da velocidade do pulsar projetada sobre a direção da linha Pulsar-Terra (praticamente imutável entre dois pulsos -- as variações na figura estão propositalmente exageradas). RV dá o movimento da estrela sem levar em conta o movimento da Terra. c é a velocidade da luz.
O intervalo de tempo entre a chegada de dois pulsos, corrigido do movimento da Terra, será dado pela equação abaixo onde RV foi separado em duas partes: a projeção sobre a linha de visada da velocidade da estrela em seu movimento ao redor do baricentro do sistema Pulsar-planeta e o movimento próprio desse sistema no espaço. O resultado final é obtido substituindo-se V pelo valor dado pelas equações da dinâmica planetária.
A variação do valor observado de Dt (corrigido) segue uma curva semelhante a uma curva de velocidades radiais, que contém informações básicas sobre o sistema -- K' e o valor do período -- semelhantes às que se obtém para estrelas observadas com espectrógrafos. Uma informação complementar é dada pela constante @ t (pois RVpr. / c<< 1).
Movimentos
de um Observador na Terra
Quando observamos o movimento de uma estrela, o que vemos é uma composição do movimento da estrela e do nosso movimento. O que medimos, tanto nas medidas astrométricas como nas de velocidade radial, são as variações do vetor Terra-estrela. Mesmo que uma estrela estivesse "imóvel" no espaço, nós a veríamos mover-se por causa do nosso movimento (o passageiro do trem ve os postes se moverem em sentido contrário ao do trem!).
Os movimentos principais são dados nas 4 figuras a seguir, nas quais indicamos as velocidades com que ocorrem:
 ....
.... ..
..
 ....
....
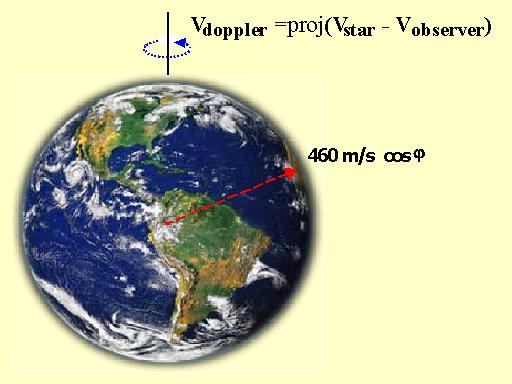
1) A Terra gira. Um observador no equador se move em um círculo de raio 6378 km e com uma velocidade de 460 m/s (muito maior do que a velocidade da estrela devida ao movimento do planeta ao seu redor.) O raio e a velocidade diminuem proporcionalmente ao cosseno da latitude do observador.
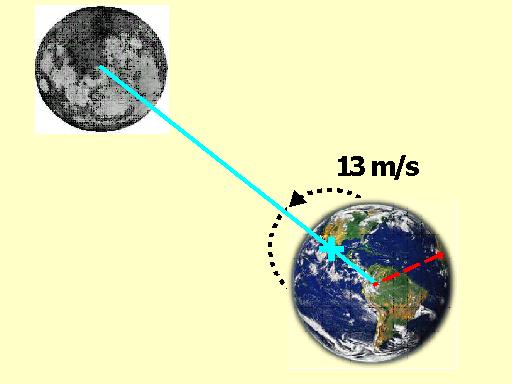
2) A Terra se move ao redor do centro de gravidade do sistema Terra-Lua. O centro de gravidade do sistema Terra-Lua está a cerca de 4700 km do centro da Terra. A velocidade da Terra nesse movimento é de 13 m/s.
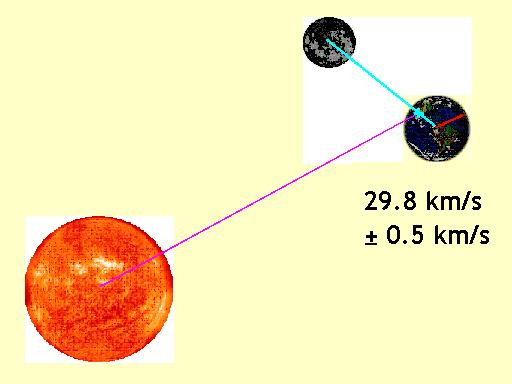
3) O Sistema Terra-Lua se move ao redor do Sol em uma elipse com semi-eixo maior 149,6 milhões de km. A velocidade da Terra na sua órbita é de aproximadamente 29,8 km/s. Ela é maior (30,3 km/s) quando a Terra está no periélio de sua órbita (dia 2 ou 3 de janeiro) e menor ( 29,3 km/s) quando a Terra está no afélio de sua órbita (6 meses depois).
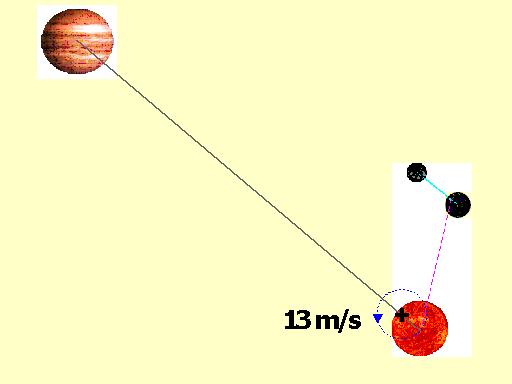
4) O Sol se move ao redor do centro de gravidade do Sistema Solar, que está situado em um ponto próximo à superfície do Sol (dentro do Sol). A posição desse ponto depende da posição de todos os planetas. A contribuição de Jupiter a esse movimento é de cerca de 13 m/s.
Nas observações astrométricas de estrelas, o único movimento considerado é o movimento ao redor do Sol (correção de paralaxe). Nas observações de objetos do sistema solar movendo-se mais próximo à Terra, o movimento ao redor do centro da Terra também deve ser considerado (paralaxe diurna).
Nas observações de velocidades radiais, os efeitos mostrados nas figuras devem ser todos considerados. Os dois programas mais usados para esse fim são o rvcorrect (do IRAF) que considera os planetas principais, mas sem levar em conta suas perturbações. De acordo com seus autores, sua precisão nominal é de 5 m/s. Um programa mais preciso existe no SAO Telescope Data Center. É o bcvcorr, que usa códigos de maior precisão para obter as posições dos planetas. Sua precisão nominal é de 42 cm/s.
Nas observações dos tempos de chegada dos pulsos oriundos de um pulsar, as precisões correspondem a velocidades radiais da ordem de 1 cm/s. Isso impõe que se considere uma longa lista de efeitos. Apenas para exemplificar, lembremos que a Terra é achatada e a aplicação da fórmula 460 cos f, exibida na figura, não é suficiente para dar a velocidade do observador com a precisão exigida no tratamento dessas observações. Outro ponto a lembrar é que o instante de chegada dos pulsos no telescópio é medido com um relógio e o relógio está se movendo com a velocidade da Terra. Essa velocidade é de um décimo de milésimo da velocidade da luz, o que já é suficiente para que seja necessário corrigir a hora medida pela expressão dada pela teoria da relatividade.
No passado várias falsas descobertas de planetas ocorreram por descuidos com a "nossa ponta do vetor". A mais celebre, no início dos anos 90, era um planeta com período 180 dias (meio ano), resultado do uso de fórmulas incorretas para exprimir o movimento da Terra ao redor do Sol. Esse é o resultado do casamento de equipamentos de última geração com rotinas de análise de dados usando fórmulas incorretas e/ou "caixas pretas" de conteúdo desconhecido.
Os sistemas planetários abrem um grande número de questões que precisam ser respondidas.
A principal é "Porque o nosso Sistema Solar é tão diferente dos demais?". Sabemos que as características dos sistemas descobertos refletem sobretudo as limitações dos métodos observacionais e não há porque nos surpreendermos que os planetas descobertos sejam grandes e que suas órbitas tenham as características que têm. Mas as teorias que foram feitas para explicá-los não se aplicam ao nosso Sistema Solar. Nos primórdios do nosso Sistema Solar também havia um disco de poeira e gás. Mas os nossos planetas gigantes são menores, estão em órbitas distantes do Sol e quase circulares. Porque não ocorreram aqui os mesmos fenômenos que nos sistemas descobertos resultaram em planetas gigantes, órbitas de dimensões reduzidas e muito excêntricas? A resposta mais óbvia é que os sistemas que estamos descobrindo são de um "tipo" diferente do nosso. Conhecemos 2 "tipos" de sistemas planetários: o nosso e os outros! O número crescente de exoplanetas descobertos e a possibilidade de um número bem maior de descobertas pela observação fotométrica automatizada de milhares de estelas, buscando detectar trânsitos de planetas, nos dirá se esses dois tipos são os únicos ou se existem outros.
Outra questão que emerge e que deverá ser respondida é a seguinte: "Os objetos que crescem dentro de um disco de poeira e gás atingindo massas estelares são iguais às estrelas anãs e sub-anãs que se formam pelo colapso de uma nuvem como as demais estrelas?".
Essas questões emergem das descobertas recentes. Mas questões mais fundamentais, e que nos vêm de tempos mais distantes também existem: "Existem outros mundos habitáveis?". Faz parte do nosso pensamento analógico considerar as nossas limitações de conhecimento como limitações da natureza. Até pouco tempo acreditávamos que planetas muito maiores do que Júpiter não poderiam existir. As teorias para explicar a existência de Júpiter não eram capazes de prever a existência de planetas maiores do que Júpiter mas nos bastavam, pois Júpiter era o maior de todos os planetas conhecidos. Hoje acreditamos que um planeta só pode ser habitável se for semelhantes ao nosso, tiver uma órbita como a da Terra e estiver ao redor de uma estrela como o Sol. Pelo menos até que a natureza nos surpreenda com uma realidade totalmente distinta!